MySQL SQRT() – Easy Way to Find the Square Root with MySQL

In this tutorial, we will learn about the MySQL SQRT() function. In high school maths, you must have come across exercises involving finding the square root of a number. Furthermore, square root finds applications across geometry, calculus, statistics, physics and many other domains which makes it one of the essential mathematical operations. For this reason and our ease, MySQL provides us with the SQRT() function. The SQRT() function is used to return the square root of a number.

Syntax of MySQL SQRT()

SQRT(number);Code language: SQL (Structured Query Language) (sql)

Where, number is the number whose square root has to be found.

Examples of MySQL SQRT()

Let’s take a look at some of the examples here.

Square Root Of A Perfect Square Number

A perfect square number is an integer that is the square of an integer. Let us consider the number 9, which is the square of 3. We will use an alias in our SELECT statement to make our output readable.

SELECT SQRT(9) AS SquareRootOf9;Code language: SQL (Structured Query Language) (sql)

And our output is,

Square Root Of Zero

The square root of zero is zero. We can see this using the below query,

SELECT SQRT(0) AS SquareRootOfZero;Code language: SQL (Structured Query Language) (sql)

And the output is,

Square Root Of Unity

How about finding the square root of one? The query is,

SELECT SQRT(1) AS SquareRootOf1;Code language: SQL (Structured Query Language) (sql)

And the output is,

Square Root Of A Non-Square Number

How about finding the square root of a number that is not a perfect square number? 18 is not a perfect square number. Let us find it’s square root using SQRT().

SELECT SQRT(18) AS SquareRootOf18;Code language: SQL (Structured Query Language) (sql)

And the output is,

Square Root Of Negative Numbers

Let us find the square root of a negative number, say -10. But, mathematical rules say that square roots of negative numbers result in imaginary numbers. So how does MySQL handle this? Well, it outputs NULL if we try to find the square root of a negative number. This is demonstrated below.

SELECT SQRT(-10) AS SquareRoot;Code language: SQL (Structured Query Language) (sql)

And the output is,

SQRT() Examples With Tables

Consider the below ‘RightAngledTriangle’ table.

How about finding the square root of all the values in the Height column? We do so using the below query,

SELECT Height, SQRT(Height) AS SquareRoot FROM RightAngledTriangle;Code language: SQL (Structured Query Language) (sql)

And the output is,

Pythagoras Theorem with MySQL SQRT()

Now let us look at a complex example. You must have studied about the Pythagoras theorem in high school. The formula for the Pythagoras theorem is,

(hypotenuse)2 = (base)2 + (height)2

You can read more about the Pythagoras theorem here.

Since our right-angled triangles already have the base and the height values in the table, we can find the value of the hypotenuse of each triangle by doing the square root of the (base)² + (height)² expression.

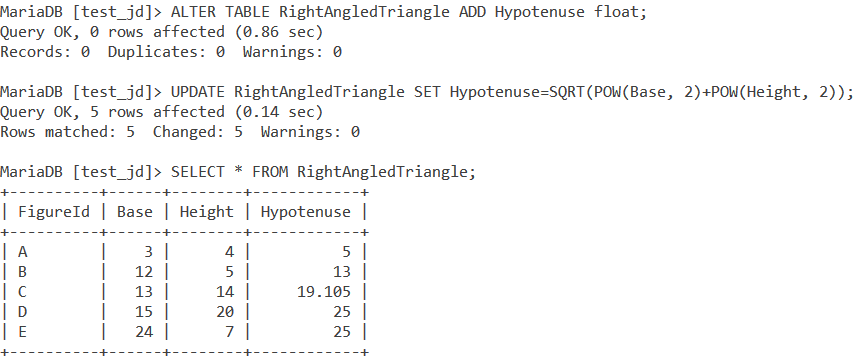
Let us create a new column named Hypotenuse and fill it with the value of the hypotenuse of the corresponding triangle using the Pythagoras theorem. We will need to use the POW() function and the ALTER and UPDATE statements.

ALTER TABLE RightAngledTriangle ADD Hypotenuse float; 
UPDATE RightAngledTriangle SET Hypotenuse=SQRT(POW(Base, 2)+POW(Height, 2)); 
SELECT * FROM RightAngledTriangle;Code language: SQL (Structured Query Language) (sql)

The ALTER statement will create a new column called Hypotenuse of the type float. The UPDATE statement will set the value of the hypotenuse. First, the POW() functions are evaluated and then added. Then, the square root of the resulting value is found out using the SQRT() function. Finally, we use the SELECT statement to display our newly updated table.

And the output is,

Conclusion

MySQL SQRT() is one of the most important mathematical operations that you will encounter while working on tables and databases related to physics and maths. Similar to the Pythagoras theorem we saw above, I would encourage you to practice other examples that demonstrate the application of SQRT().