In this tutorial, we will learn about the MySQL COS() function. While studying high school mathematics, you must have studied how to find the cosine of an angle. Finding the cosine of an angle is an important trigonometric operation which finds use in mathematics, physics and so on.
Recommended read – MySQL SIN() to find the sine of angles
MySQL provides us with the COS() function to find the cosine of a value where the value is given in radians. Let us look at the syntax of the COS() function followed by some examples.
Syntax of MySQL COS()
COS(number);Code language: SQL (Structured Query Language) (sql)Where ‘number’ is the measure of an angle in radians whose cosine is to be found.
Examples of MySQL COS()
Let us start with some basic examples. Consider the below queries.
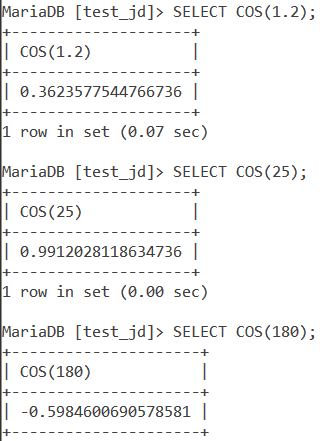
SELECT COS(1.2);
SELECT COS(25);
SELECT COS(180);Code language: SQL (Structured Query Language) (sql)And we get the output as –
MySQL COS() With Negative Values
We can also pass negative values to the MySQL COS() function. Let us see this using the below examples.
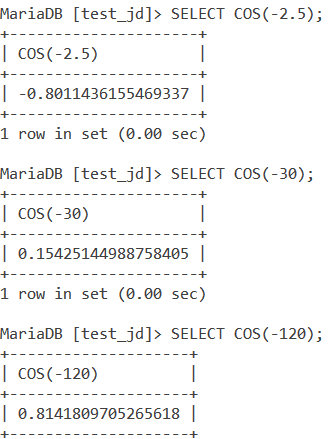
SELECT COS(-2.5);
SELECT COS(-30);
SELECT COS(-120);Code language: SQL (Structured Query Language) (sql)And we get the output as –
MySQL COS() With PI()
We can also pass mathematical functions like PI(), as arguments to MySQL COS(). After all, most radian values are expressed in terms of 𝜋. Let us see this using the below example.
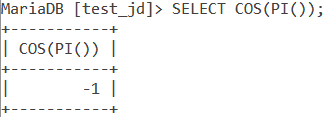
SELECT COS(PI());Code language: SQL (Structured Query Language) (sql)And the output is –
COS() With Expressions
We can pass expressions as arguments to COS() as well as use COS() in expressions. Consider the below expression.
1 - 3 cos 𝜋/2
Let us write a query for this.
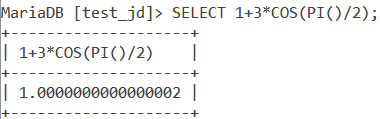
SELECT 1+3*COS(PI()/2);Code language: SQL (Structured Query Language) (sql)And the output is,
MySQL COS() With POW()
One of the mathematical functions you’ll find using the most with the COS() function is POW(). Let us take this opportunity to see an example of the same. Consider the below expression.
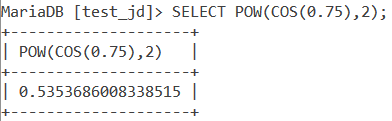
cos2 0.75
We solve this using the below query.
SELECT POW(COS(0.75),2);Code language: SQL (Structured Query Language) (sql)And we get the output as follows –
COS() With Tables
Let us work with tables now. Consider the below ‘Angles’ Table where the Angle column contains the measure of angles in radians.

Simple Example
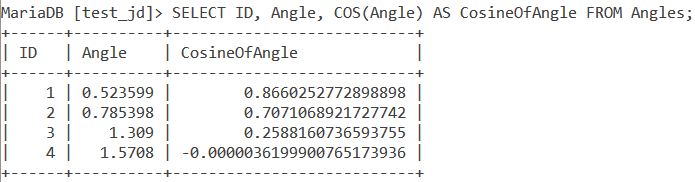
Using the SELECT statement, the COS() function and an alias called CosineOfAngle, let us display the table along with the cosine of every corresponding angle. We do this using the below query.
SELECT ID, Angle, COS(Angle) AS CosineOfAngle FROM Angles;Code language: SQL (Structured Query Language) (sql)And we get the output as –
UPDATE Statement With SIN()
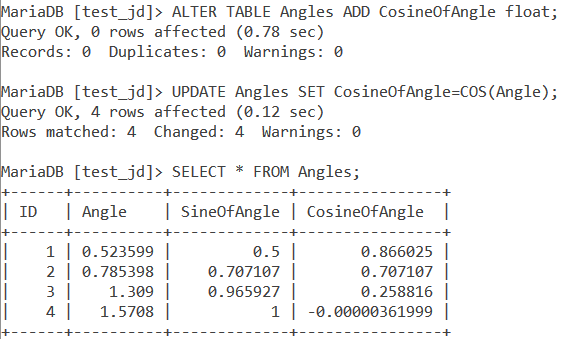
Let us now create a column called CosineOfAngle which stores the cosine of every angle in the Angles table. We will use the ALTER and UPDATE statements for this task. Let us take a look at the queries.
ALTER TABLE Angles ADD CosineOfAngle float;
UPDATE Angles SET CosineOfAngle=COS(Angle);
SELECT * FROM Angles;Code language: SQL (Structured Query Language) (sql)We add a column named CosineOfAngle of the data type float using the ALTER statement. Next, using the UPDATE statement, we populate the NULL values in the CosineOfAngle column with the cosine of the angles from the Angle column. Finally, using the SELECT statement, we display our newly updated table. The output is as follows.
A Complex Example
If you have studied trigonometric formulas, you must have definitely come across the below formula.
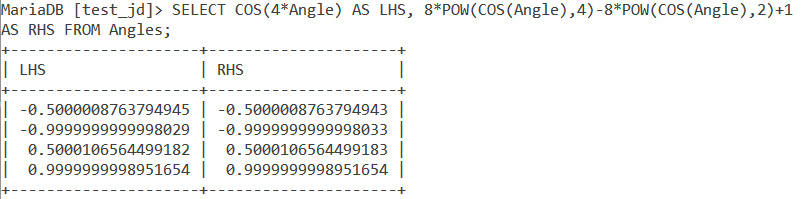
cos 4A = 8cos4 A - 8cos2 A + 1
How about proving if this formula is true using the ‘Angles’ table and the COS() function. Bear with me because we are gonna be writing a really complicated query using all the concepts we saw earlier. We will give ‘cos 4A’ an alias called LHS and ‘8cos4 A – 8cos2 A + 1’ an alias called RHS.
SELECT COS(4*Angle) AS LHS, 8*POW(COS(Angle),4)-8*POW(COS(Angle),2)+1 AS RHS FROM Angles;Code language: SQL (Structured Query Language) (sql)The first part of the above query is used to evaluate the ‘cos 4A’ part of the formula. This is given an alias called LHS. The second part of the query is given an alias called RHS. It evaluates ‘8cos4 A – 8cos2 A + 1’. Read the query once more to understand it better by breaking it one term at a time.
We get the output as,
Conclusion
Finding the cosine of an angle is an important trigonometric operation. You will find yourself using the COS() function every time you deal with data with trigonometric operations.
References
- MySQL Official Documentation on
COS().
