MySQL SIN() – How to find the sine of angles in MySQL?

By /
SIN Function

In this tutorial, we will learn about the MySQL SIN() function. While studying high school mathematics, you must have studied how to find the sine of an angle. Finding the sine of a number is an important trigonometric operation which finds use in mathematics, physics and so on. MySQL provides us with the SIN() function to find the sine of a value where the value is given in radians. Let us look at the syntax of the SIN() function followed by some examples.

Syntax of MySQL SIN()

SIN(number);Code language: SQL (Structured Query Language) (sql)

Where ‘number’ is a value in radians whose sine is to be found.

Examples of MySQL SIN()

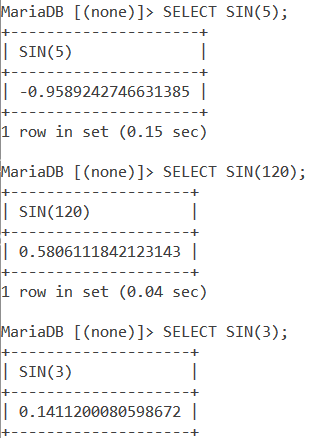
Let’s kick things off with a couple of basic examples of MySQL SIN(). Let us find the sine of 5, 120 and 3. Our queries are – 

SELECT SIN(5); 
SELECT SIN(120); 
SELECT SIN(3);Code language: SQL (Structured Query Language) (sql)

And the output is,

Sin Basic Examples

MySQL SIN() With Negative Values

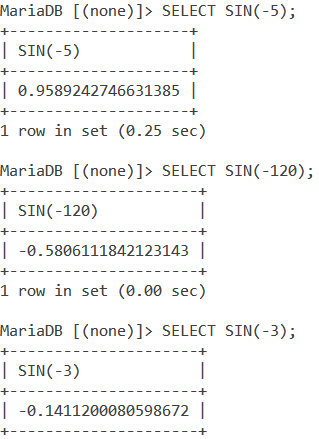
We can also use negative values with the SIN() function. Let us demonstrate this using the following queries.

SELECT SIN(-5); 
SELECT SIN(-120); 
SELECT SIN(-3);Code language: SQL (Structured Query Language) (sql)

And the output is,

MySQL SIN Negative

SIN() Of PI()

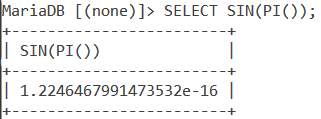
We can also pass a function within SIN(). Let us find the sine of 𝜋 using the PI() function. We do this using the below query.

SELECT SIN(PI());Code language: SQL (Structured Query Language) (sql)

And the output is,

MySQL SIN Pi

Using Expressions with MySQL SIN()

We can also use expressions with the SIN() function. Suppose we have the following expression:

1 – sin 𝜋/6

We do this using the below query,

SELECT 1-SIN(PI()/6);Code language: SQL (Structured Query Language) (sql)

First, the PI()/6 expression is evaluated. Next, the expression finds the sine of the resulting value and then subtracts it from 1. We get the output as,

MySQL SIN Expression

POW() with SIN()

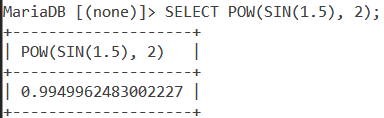
One of the mathematical functions you’ll find using the most with the SIN() function is POW(). Let us take this opportunity to see an example of the same. Consider the below expression.

sin2 1.5

We solve this using the below query.

SELECT POW(SIN(1.5), 2);Code language: SQL (Structured Query Language) (sql)

First, the SIN() function gets evaluated. And then, we square the resulting value with the POW() function. Finally, we get the output as follows.

Sin Pow

SIN() With Tables

Consider the below ‘Angles’ table. The Angles Table contains the ID of an angle and its value in radians.

Angles Table
Angles Table

Using the SELECT statement, the SIN() function and an alias called SineOfAngle, let us display the table along with the sine of every corresponding angle. We do this using the below query.

SELECT ID, Angle, SIN(Angle) AS SineOfAngle FROM Angles;Code language: SQL (Structured Query Language) (sql)

And we get the output as follows,

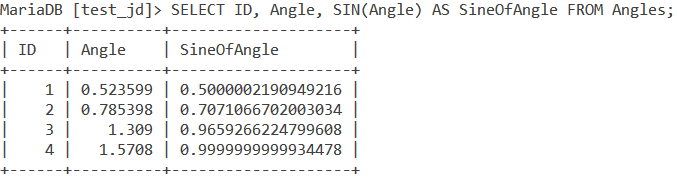
Sin Table Example 1

UPDATE Statement With SIN()

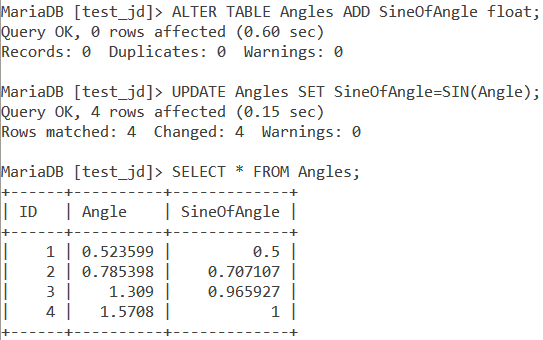
Let us now create a column called SineOfAngle which stores the sine of every angle in the Angles table. We will use the ALTER and UPDATE statements for this task. Let us take a look at the queries.

ALTER TABLE Angles ADD SineOfAngle float; 
UPDATE Angles SET SineOfAngles=SIN(Angle); 
SELECT * FROM Angles;Code language: SQL (Structured Query Language) (sql)

We add a column named SineOfAngle of the data type float using the ALTER statement. Next, using the UPDATE statement, we populate the NULL values in the SineOfAngle column with the sine of the angles from the Angle column. Finally, using the SELECT statement, we display our newly updated table. The output is as follows.

Sin Table Example 2

A Complex Example

Okay. If you have studied trigonometric formulas, you must have definitely come across the below formula.

sin 3A = 3sin A - 4sin3 A

Complicated, I know. So how about proving if this formula is true using the ‘Angles’ table and the SIN() function. Bear with me because we are gonna be writing a really complicated query using all the concepts we saw earlier.

SELECT 3*SIN(Angle), 3*SIN(Angle)-4*POW(SIN(Angle), 3) FROM Angles;Code language: SQL (Structured Query Language) (sql)

The first part of the above query is used to evaluate the ‘sin 3A’ part of the formula. The second part of the SELECT statement is used to evaluate ‘3sin A – 4sin3 A’. Read the query once more to understand it better by breaking it one value at a time.

We get the output as,

Sin Table Example 3

As you can see, the values in both columns match. Hence, we proved the formula is true using MySQL SIN().

Conclusion

Finding the sine of an angle is an important trigonometric operation. You will find yourself using the SIN() function every time you deal with data with trigonometric operations.

References