MySQL BIN(), OCT() and HEX() Functions

By /
Bin Oct Hex

In this tutorial, we will learn about the MySQL BIN(), OCT() and HEX() functions. As you would have known by now, computers do not understand the language of humans. They only understand 0s and 1s. Numbers in the computer language often have a base or radix, such that all numbers present in that number system range from zero to (base-1). Let me elaborate more on this.

Introduction

In computer language, there are four popular number systems –

  • The decimal number system – The base is 10.
  • The binary number system – The base is 2.
  • The octal number system – The base is 8.
  • The hexadecimal number system – The base is 16.

These numbers find a lot of applications in electronic and digital circuits which, long story short, form the basis of our modern-day computers. The decimal number system is the number system which we use in our everyday life. Let us explore the other number systems using the MySQL BIN(), OCT() and HEX() functions.

MySQL BIN()

The MySQL BIN() function is used to convert a number (from the decimal number system) to its binary equivalent. The returned value is a string.

Following is a table that shows the binary representation of numbers from 0 to 8. Note that numbers greater than 8 also have binary equivalent values. This table is just for example purposes.

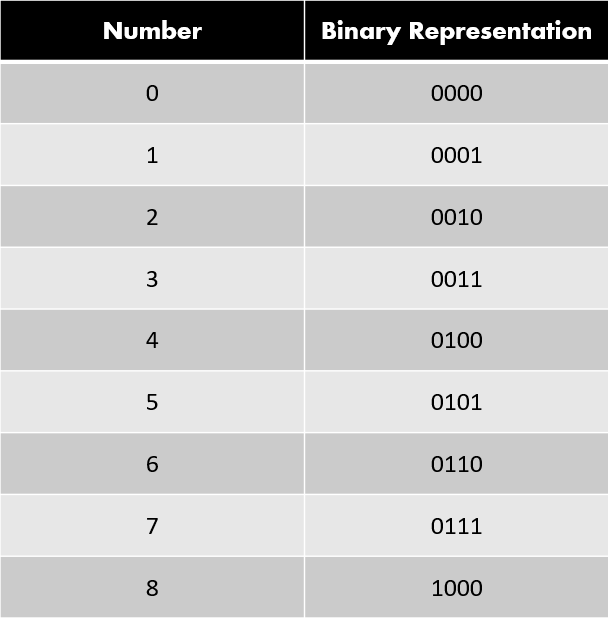
Binary Representation Of Numbers
Binary Representation Of Numbers

You can read more about the math about the binary representation of numbers here.

Syntax of MySQL BIN()

BIN(number)Code language: SQL (Structured Query Language) (sql)

Where ‘number’ is a number whose binary representation is to be found out.

Example of MySQL BIN()

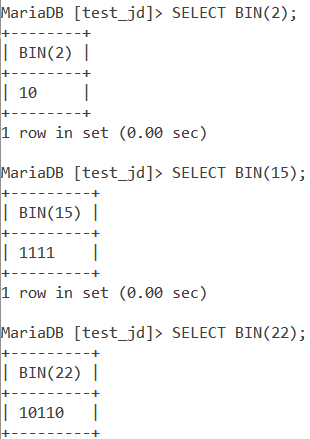
Let us find the binary representation of the following numbers – 2, 15 and 22. The queries are –

SELECT BIN(2); 
SELECT BIN(15); 
SELECT BIN(22); Code language: SQL (Structured Query Language) (sql)

And we get the output as follows.

Bin Basic Example

MySQL OCT()

The MySQL OCT() function is used to convert a number (from the decimal number system) to its octal equivalent. The returned value is a string.

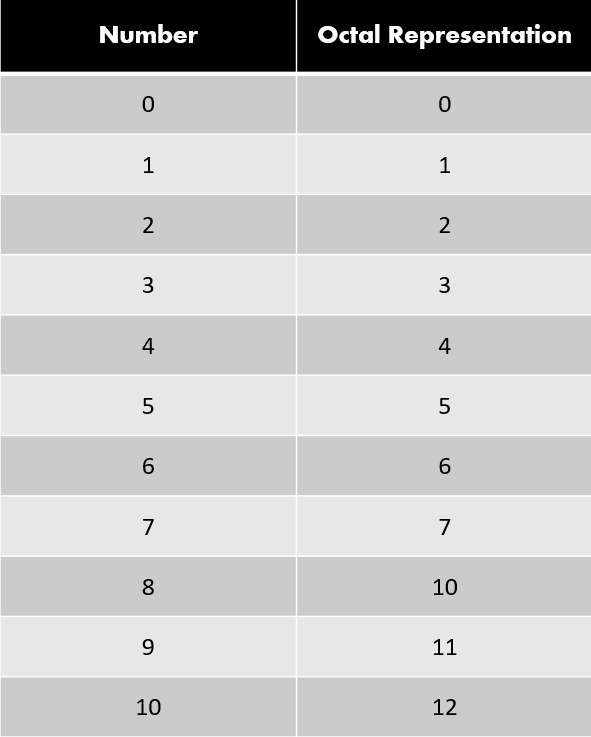
Following is a table that shows the octal representation of numbers from 0 to 10. Note that numbers greater than 10 also have octal equivalent values. This table is just for example purposes.

Octal Representation Of Numbers
Octal Representation Of Numbers

Syntax of MySQL OCT()

OCT(number)Code language: SQL (Structured Query Language) (sql)

Where ‘number’ is a number whose octal representation is to be found out.

Basic Example of MySQL OCT()

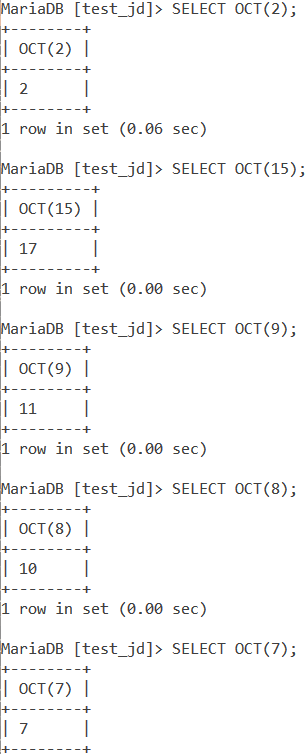
Let us find the octal representation of the following numbers – 2, 15, 9, 8 and 7. The queries are –

SELECT OCT(2); 
SELECT OCT(15); 
SELECT OCT(9); 
SELECT OCT(8); 
SELECT OCT(7);Code language: SQL (Structured Query Language) (sql)

And we get the output as follows.

Oct Basic Example

MySQL HEX()

The MySQL HEX() function is used to convert a number (from the decimal number system) to its hexadecimal equivalent. The returned value is a string.

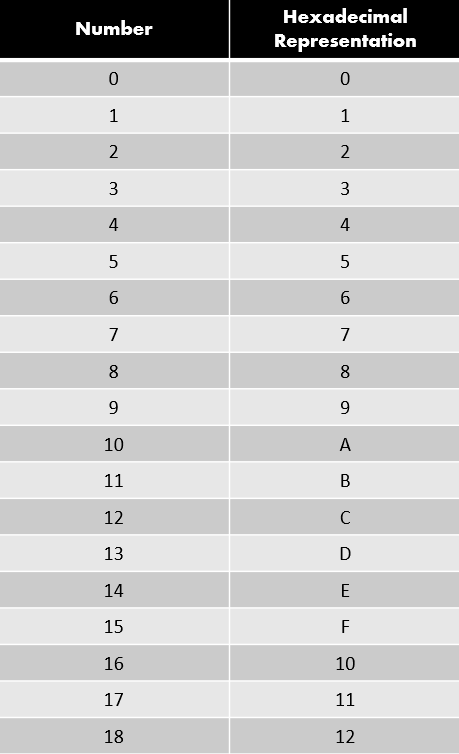
Following is a table that shows the hexadecimal representation of numbers from 0 to 18. Note that numbers greater than 18 also have hexadecimal equivalent values. This table is just for example purposes.

Hexadecimal Representation Of Numbers
Hexadecimal Representation Of Numbers

Syntax of MySQL HEX()

HEX(number)Code language: SQL (Structured Query Language) (sql)

Where ‘number’ is a number whose hexadecimal representation is to be found out.

Basic Example of MySQL HEX()

Let us find the hexadecimal representation of the following numbers – 7, 11, 17, 22 and 28. The queries are –

SELECT HEX(7); 
SELECT HEX(11); 
SELECT HEX(17); 
SELECT HEX(22); 
SELECT HEX(28);Code language: SQL (Structured Query Language) (sql)

And we get the output as follows.

Hex Basic Example

MySQL BIN(), OCT() and HEX() With Tables

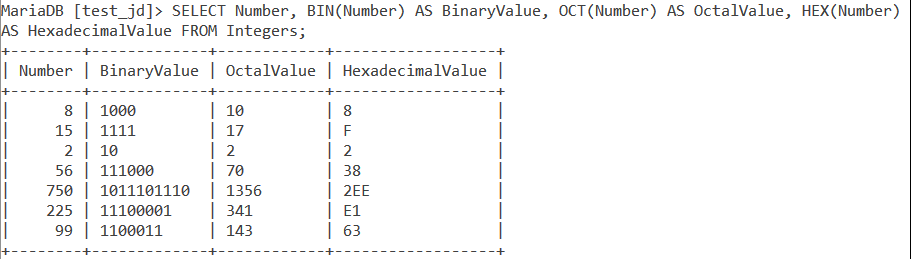
Consider the below ‘Integers’ table. It has only one column – the Number column which stores an integer.

Integers Table
Integers Table

Using the SELECT Statement, aliases and the BIN(), OCT() and HEX() functions; let us find the binary, octal and hexadecimal equivalent values of the values in the Number column. The query is –

SELECT Number, BIN(Number) AS BinaryValue, OCT(Number) AS OctalValue, HEX(Number) AS HexadecimalValue FROM Integers;Code language: SQL (Structured Query Language) (sql)

And we get the output as –

Table Example Bin Oct Hex

Conclusion

Converting from one base representation to another is an important operation especially with data involving the electronics and digital circuits domain. I would encourage you to read more of these number systems and functions.